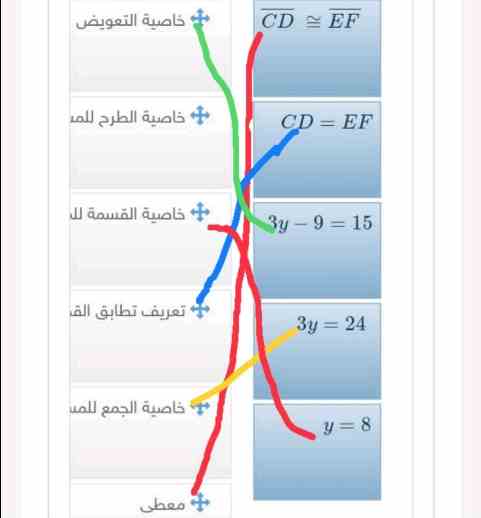
حل سؤال اقرن العمود الأول بما يناسبه من العمود الثاني وذلك لإثبات أن: إذا كان CD ≅ EF فإن y=8
اهلا بكم اعزائي زوار شبكة محتويات التعليمية
اجابة سؤال اقرن العمود الأول بما يناسبه من العمود الثاني وذلك لإثبات أن: إذا كان CD ≅ EF فإن y=8
اقرن العمود الأول بما يناسبه من العمود الثاني وذلك لإثبات أن: إذا كان CD⎯ ≅EF⎯⎯ فإن y=8
حل سؤال اقرن العمود الأول بما يناسبه من العمود الثاني وذلك لإثبات أن: إذا كان CD ≅ EF فإن y=8 بيت العلم
التعليم هو الشي الأساسي للوصول إلى معرفة لا حدود لها لذلك فإننا على موقع المتوفر دائمًا نقوم بتوفير الإجابة على أسئلتكم وتقديم الدعم اللازم لكم سواء كنت تواجه صعوبة في فهم مفهوم معين لمختلف المواد الدراسية، وكان احد أبرز الاسئلة التي سنقوم بالإجابة عليها هو :
اقرن العمود الأول بما يناسبه من العمود الثاني وذلك لإثبات أن: إذا كان CD ≅ EF فإن y=8 ؟
الاجابة الصحيحة هي:
في عالم الرياضيات، تعتبر المسائل التي تتضمن إثبات تطابق الأشكال والمتغيرات من الأسئلة الشائعة التي تحتاج إلى تفكير منطقي وتطبيق للمبادئ الأساسية. لإثبات أن \( y = 8 \) إذا كان \( CD \cong EF \)، يجب اتباع سلسلة من الخطوات المنطقية التي تبدأ بالمعطيات وتنتهي بالنتيجة المطلوبة.
إقرأ أيضا:حل سؤال كان عامة المشركين يقرون بتوحيدالخطوات المنطقية للإثبات هي كالتالي:
- 1. نبدأ بالمعطى \( CD \cong EF \).
- 2. نطبق تعريف تطابق القطع المستقيمة لنقول أن \( CD = EF \).
- 3. نستخدم خاصية التعويض للمساواة لنقول أن \( 3y – 9 = 15 \).
- 4. نطبق خاصية الجمع للمساواة لنحصل على \( 3y = 24 \).
- 5. وأخيرًا، نستخدم خاصية القسمة للمساواة لنجد أن \( y = 8 \).
وفي نهاية المقال نتمني ان تكون الاجابة كافية ونتمني لكم التوفيق في جميع المراحل التعليمية , ويسعدنا ان نستقبل اسئلتكم واقتراحاتكم من خلال مشاركتكم معنا
ونتمني منكم ان تقومو بمشاركة المقال علي مواقع التواصل الاجتماعي فيس بوك وتويتر من الازرار السفل المقالة